B03 应用黏弹性分析于预测射出产品之流动残留应力

1. 前言 

射出成型产品中存在的残余应力主要由两个原因所导致，一为充填阶段之由流动残余应力所引发之分子排向，二为冷却阶段不均匀收缩所产生之热残余应力。流动残余应力主要受到在塑料充填流动的过程中高剪切率所导致，而在充填之后的冷却与脱模阶段持续被释放或冻结。热残余应力则主要由高温的塑料材料冷却到玻璃转移温度([attach]9254[/attach] image002.gif)后的不均匀的体积收缩与密度变化所生成。

分子排向与流动残余应力在充填阶段与保压阶段是属于高分子黏弹性的行为。在温度高于玻璃转移温度之下，塑料处于液态的阶段，高分子链将依据流动方向产生相应对的配向。而射出成型过程中高冷却率下的快速固化将使得这些应力与分子排向无法被完全的松弛及释放。 

流动残余应力一般认为比热残余应力小，然而流动残余应力与高分子的冻结排向息息相关，在现今的技术中利用流动残余应力提供与分子排向的关联是较为可行的方案。而高分子冻结排向影响了非等向性的机械性质、热性质与光学性质，并影响了之后的尺寸稳定度，因此流动残余应力之重要性是无法忽略。

流动残余应力在薄件成型中相对于热残余应力更是扮演主导性的角色，因为薄件的冷却太快使得分子排向不完全松弛的量增加，而薄件也将产生比较少的体积收缩率及较小的热残余应力。一般在模穴表面的固化层是热的不良导体，使得在模穴核心的温度可以维持高温，使得分子排向在这区域可以被松弛释放，然而在薄件成型中，整个产品在很短的周期下冷却而快速冻结，因此在薄件中流动应力的释放较少而占有主导的地位，而热残余应力则在厚件中占有主导的地位。

未来的产品发展，在实际应用的许可下，逐渐走向轻薄短小的方向发展，消费型产品可以更轻便贴近用户需求，而泛用型产品可以尽量节省材料。因而预期在未来，在充填过程中狭小的流动空间将会使得流动残余应力所导致的问题逐日严重，也将逐渐被重视。以往黏弹性分析发展受限于计算耗时与求解过程不稳定，不但只能发展于2.5D薄壳理论下，且局限在学术上的讨论与研究。幸而在计算机计算技术逐渐加快与数值模拟方法不断发展下，发展出足以应付复杂工业案例及真实三维仿真过程的黏弹性分析已经不再是遥不可及。

本文整合真实三维热流求解核心与黏弹性模型仿真熔胶在射出成型制程中的流动残余应力。本文以一长方形平板的模穴充填分析作为探讨，最后再以一工业界的产品之实验与仿真的比较作为现有数值方法的可信度的展示，其结果可进一步以应用至光学性质的预测与翘曲行为的影响等。

2. 数值模型

假设高分子熔胶行为为黏弹性流体，非恒温的三维流动之数学方程式可以表示如下：

体积分率函数 ，用来追踪波前的移动。 代表为空气， 为高分子熔胶，而波前的位置就是落在格点中体积分率为 的区域。体积分率随着时间的推进可以表示为下列的传输方程式：

在模穴入口处之进胶面给定充填流率或者射出压力，在模壁给定无滑移边界条件，而特别需要注意的是，在体积分率的传输方程式中，由于是双曲线式之方程式，只需给定入口边界条件。

本文，利用有限体积法(Finite Volume Method )求解各流场与应力相关之统驭方程式，而数值核心在文献[2]已经被验证可以成功的应用在射出成型充填模拟，许多实验与测试也确认了此数值核心在可靠度上与效率上的表现。

3. 结果与讨论

本文首先采用一Lehigh U.[4]所用之长方形薄板，作为与实验比对之案例。几何外观分别为3.3 mm (厚度) x 101.6 mm (长度) x 50.8 mm (宽度)。材料选定为PS Styron 666D，料温与模温分别设定为200℃ and 52℃，充填时间为0.75秒，保压时间则为20秒。相关材料与加工条件之信息整理如表1 。而此案例之网格，为厚度方向上有20层的混合三维元素，如图1红色框架之圈选部分所示。本文之后会讨论厚度方向一些变量之分布，切面位置如图1蓝色框架之圈选部分。

图2为波前时间位置之仿真结果，由左侧中心进胶，波前分布呈现稳定与平衡，没有因流道产生流动不平衡之现象。

由于此案例之主要流动方向为x方向，将流动残余应力之模拟结果，从六个应力变量中选出三个与x相关之分量( 与  

)。应力分量的下标中，以 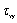为例(如图3)，第一个指标是指应力作用于垂直于x轴之平面(此平面之向量为x方向)，第二个指标是指应力作用方向为y方向，而应力作用方向如果与坐标方向相同则为正值。此定义下之变形，将为右上方向与左下方向之拉伸与剪切变形。

图4 (a)为 之分布，其值皆为正值，可以代表高分子在主要流动方向(x方向)受到拉伸应力。而读者可以看出靠近浇口处其 

应力最高，这是由于靠近浇口处的剪切率与速度场变化最大，高分子受到流动造成的排向与拉伸应力也最大。

图4 (b)为 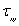之分布，其值在浇口上半部为正值，下半部为负值。显示在进入浇口后，在上半部区域高分子呈现约45度向上剪切与拉伸，在下半部约45度向下剪切与拉伸,由图4(a)亦可看出。图4 (c)为 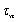之分布，由于厚度方向受到模壁影响较明显，呈现明显的上半部负值（向右下方剪切变形），下半部正值（即向右上方剪切变形）。

图5 呈现出Von Mises stress( 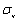)的分布，主要用来代表应力张量的量值大小，本文所得到的 数值结果，最大值在靠近浇口的地方，离浇口越近其值越高，如图5(a)。而以厚度方向观察，靠近表面的地方，由于受到模壁影响，有高剪切应力下所导致的分子排向以及受到模壁快速冷却的冻结，呈现靠近模壁的地方，流动残余应力较大的情形，如图5(b)。

图6为流动残余应力中之最大主轴应力，或者称之为最大正向应力，在射出成型制程中此值为高分子受到轴向之最大拉伸应力，可以代表塑料之分子排向。由图6(b)厚度方向之分布可以看出，靠近模壁排向明显，而中心区域排向不明显而较为混乱。

图7为厚度方向松弛时间分布，松弛时间为黏弹性计算之重要材料参数，一般为温度与剪切率的函数。松弛时间代表在不受到外力下，应力量值释放至原本的一半所需之时间，温度越低时，材料表现出固态之弹性效应越强，松弛时间也越高。由图7(a)流动结束时之松弛时间分布，可以看到受到模壁低温的快速冷却影响，模壁表面之松弛时间很高，此区域亦可以判断为流动阶段之固化层。图7(b)保压结束时之松弛时间分布，可以看出随着时间的增加，固化层也在增厚。

另外，图8 乃利用一工业界的实际产品作为分析案例，以验证本文目前所整合数值演算方法的延伸性。图8(a) 是一个ABS的按键产品，在经过沉进于冰醋酸一段时间后，表面的残余应力受到松弛，分子将会改变区域表面的颜色，而呈现白色，是一般方便使用之半定性观察残余应力与分子排向之方法。因此图8(a) 的白色区域可以说是残余应力与分子排向较高之区域。而数值模拟所得到的结果如图8(b)，与实验观察有相当程度的吻合。